Uma diagonal de um polígono é um segmento de reta entre dois vértices não consecutivos do polígono.

Cálculo do número de diagonais de um polígono

A fórmula para se calcular a quantidade de diagonais "P" que tem em um polígono de "n" lados é a seguinte:

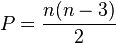
É necessário salientar que o triângulo não possui diagonais, e o pentágono é o único polígono, cujo número de diagonais é o mesmo que o número de lados.

Desenvolvendo a fórmula do cálculo do número de diagonais de um polígono

Tendo o retângulo acima como base para o estudo da fórmula, isolamos (limitamos nossa atenção) a um dos vértices, tomemos, por exemplo, o vértice A. Para esse vértice, somente é possível fazer diagonal com outro vértice não adjacente a ele, nesse caso, o vértice C. Os vértices B e D devem ser desconsiderados pois formam com o A dois dos lados do polígono.

Criamos uma fórmula que descreva a afirmação anterior:

Seja P o número de diagonais possíveis ao vértice A, desconsiderando os 3 (três) vértices com os quais não é possível ligar uma diagonal, a saber: B, D e o próprio A.

P = n − 3

Onde 'n' é o número de vértices do polígono.

Aplicando essa fórmula ao retângulo acima, temos: P = 4 − 3 portanto, para o vértice A uma só diagonal.

Se temos uma fórmula que calcula o número de diagonais para um vértice do polígono, bastaria então multiplicar essa fórmula pelo número de vértices desse polígono para aplicá-la aos outros vértices, porém, o que se observa é que o resultado será sempre o dobro do número de diagonais do polígono, veja:

P = n(n − 3)

P = 4(4 − 3) = 4

Isso se deve ao fato que uma diagonal é sempre "compartilhada" por dois vértices, daí a necessidade de se dividir por 2. Então:

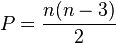
ou ainda:

Fica fácil agora entender matematicamente o porquê do triângulo não ter diagonais, uma vez que serão desconsiderados sempre 3 vértices: o próprio e os dois adjacentes.